Solitary Wave Theory
2.4.1 Solitary Wave
The nonlinear evolution equations that describe the wave process in dispersive and dissipation media have soliton-like solutions for these waves [6]
2.4.2 Soliton
A solitary wave that asymptotically maintains its shape and velocity when interacting nonlinearly with other solitary waves is known as a soliton [43]. The characteristics of Soliton are as follows:
1. Their form is permanent.
2. They are confined to a certain area.
3. Aside from a phase shift, they can interact with other solitons and come out of the collision unaltered.
4. A fine balance between dispersive and nonlinear effects results in soliton.
2.4.3 Travelling Wave
A traveling wave [43] is one in which the medium moves in the direction of the wave's propagation. When studying nonlinear differential equations, traveling waves occur. These waves are represented by the form
![]()
and ![]() is the speed of wave propagation. For
is the speed of wave propagation. For ![]() , the wave moves in the positive
, the wave moves in the positive ![]() direction whereas the wave moves in the negative
direction whereas the wave moves in the negative ![]() direction for
direction for ![]() .
.
2.4.4 Types of Travelling Wave Solutions
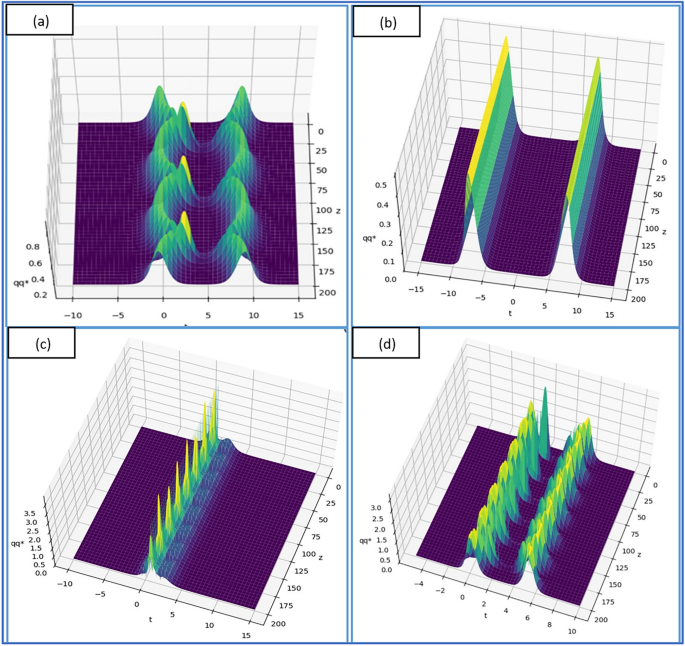
In solitary wave theory, traveling wave solutions,which come in a variety of forms are very significant. Six distinct kinds of traveling wave solutions will be discussed here, along with their corresponding figures.
Definition 2.17. Localized traveling waves with constant forms and speeds that asymptotically zero at long distance solutions are known as solitary waves [43]. One particular type of solitary wave is called a soliton. A spatially localized solution is the soliton solution
The KdV equation is a pioneer model for analytic bell-shaped ![]() solitary wave solutions.
solitary wave solutions.
Definition 2.18. Traveling waves that rise or fall from one asymptotic condition to another are known as kink waves [43]. At infinity, the Kink solution gets closer to a constant
Definition 2.19Periodic waves [43] are periodic traveling waves, such cos(x-t). Periodic solutions are provided by the standard wave Below is a graphic representation.
representation is given below
Definition 2.20. The solitary wave solutions are called peakons [43]. With the exception of a peak at one corner of its crest, the traveling solutions in this instance are smooth. Peakons are solutions that, following interaction, maintain their speed and shape. After investigation, peakons were divided into two categories: periodic peakons and peakons with exponential decay. Below are a few graphical depictions of peakons.
Definition 2.21. Another type of solitons that have cusps at their crests are called cuspons [43]. The derivative at a Cuspons jump diverges, in contrast to Peakons, where the derivative at the peak differs only by a sign.
.
Definition 2.22. Each compacton is a soliton constrained to a finite core, making it a new form of soliton with compact spatial support. One of the following methods can be used to characterize the properties of compactons [43]:
1. Solitons with a finite wavelength are called compactons.
2. Single waves with compact support are called compactons.
3. Solitons without an exponential tail are called compactons.
4. The lack of endless wings distinguishes compactons from soliton.
5. Compactons are strong solutions that resemble solvon.
Below is a graphic representation.
2.5 Some Basic Definitions of Wavelets Theory
2.5.1 History
In the 1980s, wavelet analysis emerged in the mostly mathematical literature, and in the 1990s, it started to be widely applied in geophysics. Wavelets can be applied to data compression, picture processing, and signal analysis. While retaining some degree of temporal or space locality, they are helpful for sorting out scale information.
2.5.2 Wavelets
"The 1980s saw the development of wavelet analysis in the mostly mathematical literature, while the 1990s saw its widespread application in geophysics. Data compression, picture processing, and signal analysis are all applications for wavelets. They are helpful for separating out scale information while preserving some degree of locality in space or time.
2.5.3 Types of Wavelets
Meyer (1993) states that two basic kinds of wavelets [44] can be taken into consideration,
1. The time-scale wavelets of Grossmann-Morlet
2. The time-frequency wavelets of Gabor-Malvar.
A "mother function" ![]() of some real variable
of some real variable ![]() is used to define time-scale wavelets.
is used to define time-scale wavelets.
![]() where
where ![]() forms an orthogonal basis.
forms an orthogonal basis.
![]() References
References
[1]S. Abbasbandy, Numerical solutions of the integral equations: Homotopy perturbation method and Adomian’s decomposition method, Appl. Math. Comput. 173(23) (2006), 493-500.
[2]Z. Avazzadeh, B. Shafiee and G. B. Loghmani, Fractional calculus for solving Abel’s integral equations using Chebyshev polynomials, Applied Mathematical Sciences, 5(45)(2011), 2207 – 2216
[3]Subhra Bhattacharya, Use of bernstein polynomials in numerical solutions of volterra integral equations: Applied Mathematical Sciences, 2(36)(2008), 1773 – 1787.
[4]Caputo, Michel, Linear model of dissipation whose Q is almost frequency independent-II. J. R. Astr. Soc. 13 (1967), 529–539.
[5]M.E. Fettis, On numerical Solution of Equations of the Abel type, Math. Comp. 18(1964), 491–496.
[6]J. Garza, P. Hall, F.H. Ruymagaart, A new method of solving noisy Abel-type equations, J. Math. Anal. Appl. 257 (2001), 403–419.
[7]P. Hall, R. Paige, F.H. Ruymagaart, Using wavelet methods to solve noisy Abel-type equations with discontinuous inputs, J. Multivariate. Anal. 86 (2003), 72–96.
[8]Li Huang, Yong Huang, Xian-Fang Li, Approximate Solution of Abel Integral Equation, Computers and Mathematics with Applications 56 (2008), 1748–1757.
[9]A. Hwang and Y. P. Shih, Solution of integral equations via Laguerre polynomials, Comput. Electr. Engrg. 9 (1982), 123–129
[10]D.A. Murio, D.G. Hinestroza, C.W. Mejia, New stable numerical inversion of Abel’s integral equation, Comput. Math. Appl. 11(1992), 3–11.
[11]D.E. Newland, An Introduction to random vibrations, spectral and wavelet analysis, longman scientific and technical, New York, (1993).
[12]R.Piessens, Computing integral transforms and solving integral equations using Chebyshev polynomial approximations, J. Comput. Appl. Math. 121 (2000),113–124.
[13]R.Piessens, P. Verbaeten, Numerical solution of the Abel integral equation, BIT 13 (1973), 451–457.
[14]A.M. Wazwaz, Partial Differential Equations and Solitary Waves Theory, HEP and Springer, Beijing and Berlin, (2009).
[15]J. Y. Xiao, L. H. Wen, D. Zhang, Solving second kind integral equations by periodic wavelet Galerkin method, Appl. Math. Comput.175(2006), 508-518.
[16] S.A.Yousefi, Numerical solution of Abel’s integral equation by using Legendre wavelets, Applied Mathematics and Computation,175 (2006), 574-580.
- Questions and Answers
- Opinion
- Motivational and Inspiring Story
- Technology
- Live and Let live
- Focus
- Geopolitics
- Military-Arms/Equipment
- Sécurité
- Economy
- Beasts of Nations
- Machine Tools-The “Mother Industry”
- Art
- Causes
- Crafts
- Dance
- Drinks
- Film/Movie
- Fitness
- Food
- Jeux
- Gardening
- Health
- Domicile
- Literature
- Music
- Networking
- Autre
- Party
- Religion
- Shopping
- Sports
- Theater
- Health and Wellness
- News
- Culture

