What is the Torsion Spring Equation and How is it Used?

A torsion spring is a mechanical component designed to store and release rotational energy. Unlike linear springs, which work through compression or extension, torsion springs operate by twisting along their axis. These springs are commonly found in devices like garage doors, watches, and clothespins, where rotational motion is essential. The torsion spring equation is fundamental in understanding how these springs behave under different forces, making it essential for designing and utilizing torsion springs effectively.
Understanding the Torsion Spring Equation
The torsion spring equation relates the torque exerted by the spring to the angle of twist and the spring constant, known as the torsion constant.
The general torsion spring formula for the torque (𝜏) in a torsion spring is given by:
𝜏=𝑘⋅𝜃
Where:
● 𝜏 is the torque exerted by the spring (measured in Newton-meters, Nm),
● 𝑘 is the torsion constant or stiffness of the spring (measured in Nm/radian),
● 𝜃 is the angular displacement or the angle by which the spring is twisted (measured in radians).
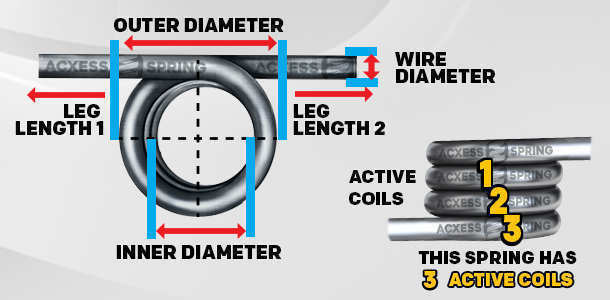
The torsion constant k indicates the spring's stiffness level and originates from material type together with dimensional and geometrical spring properties. The combination of rigid material and large spring diameter proportions directly results in a greater torsion constant value. Spring deformation from its natural position is measured through the angle value θ\thetaθ.
The twisting resistance ability of springs defines the distinctive feature of torsion springs. The application of torque enables you to store potential energy within the spring until the torque removal produces rotational motion.
Deriving the Energy Stored in a Torsion Spring
In addition to calculating torque, the energy stored in a torsion spring is another important aspect. The formula for the stored energy (U) in a spring torsion is:
U = (1/2) * k * 𝜃²
Where:
● U is the stored potential energy (measured in joules),
● k is the torsion constant,
● 𝜃 is the angular displacement in radians.
The stored spring energy exhibits a direct relationship to the squared value of angular displacement. When the spring reaches advanced angles during twisting it develops high amounts of stored energy according to its design equation.

Practical Uses of the Torsion Spring Equation
Different engineering and mechanical applications deploy the torsion spring equation regularly for their operations. A couple of fundamental applications of this equation include:
- Designing Mechanisms: Engineers who work in mechanical design employ the torsion spring equation to establish the suitable spring constant together with torsion angle for their applications. Garage door springs must have enough strength to raise heavy doors whereas proper torque application at correct angles balances door weight.
- Automated Systems: The torsion spring equation enables proper system functionality in automated rotation equipment such as watches and automotive parts where it provides precise rotational force at specific angular positions.
- Coil Springs and Torsion Springs: Perfect examples of torsion springs are coil springs that require equivalent equations to analyse their response to loading forces. Application-specific selection of springs requires knowing that linear force applications use coil springs, but torsion springs work uniquely for rotational forces.
Unit of Spring Constant in Torsion Springs
The unit of spring constant of measurement that combines Newton meters with radians (Nm/radian). A radian of spring rotation needs an equivalent torque force measured in Newton meters per radian. A higher value of the torsion constant makes the spring more rigid so it withstands applied torque at a greater level of resistance.
Conclusion
The torsion spring equation is a vital tool for understanding the mechanics behind torsion springs. It enables engineers and designers to calculate and optimize the performance of torsion springs. Whether you are using a torsion spring calculator or designing from scratch, understanding these key concepts can lead to safer and more effective use of torsion springs in mechanical systems.
- Questions and Answers
- Opinion
- Motivational and Inspiring Story
- Technology
- Live and Let live
- Focus
- Geopolitics
- Military-Arms/Equipment
- Ασφάλεια
- Economy
- Beasts of Nations
- Machine Tools-The “Mother Industry”
- Art
- Causes
- Crafts
- Dance
- Drinks
- Film/Movie
- Fitness
- Food
- Παιχνίδια
- Gardening
- Health
- Κεντρική Σελίδα
- Literature
- Music
- Networking
- άλλο
- Party
- Religion
- Shopping
- Sports
- Theater
- Health and Wellness
- News
- Culture

